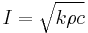Volumetric heat capacity

Volumetric heat capacity (VHC), also termed volume-specific heat capacity, describes the ability of a given volume of a substance to store internal energy while undergoing a given temperature change, but without undergoing a phase change. It is different from specific heat capacity in that the VHC depends on the volume of the material, while the specific heat is based on the mass of the material. If given a specific heat value of a substance, one can convert it to the VHC by multiplying the specific heat by the density of the substance.[1]

Dulong and Petit predicted in 1818 that ρcp would be constant for all solids. In 1819 they found that the most constant quantity was the heat capacity of solids adjusted by the presumed weight of the atoms of the substance, as defined by Dalton (the Dulong-Petit law). This is the heat capacity per atomic weight, which suggests that it is the heat capacity per atom which is closest to being a constant in solids. The heat capacity on a volumetric basis actually varies from about 1.2 to 4.5 MJ/m³K, mostly due to differences in the physical size of atoms (if all atoms were the same size, the two kinds of heat capacity would be equivalent). For liquids, the volumetric heat capacity is in the range 1.3 to 1.9 MJ/m³K.

For monatomic gases (like argon) at room temperature and constant volume, it is about 0.5 kJ/m³K. The much lower value for gases results mostly from the fact that gases under standard conditions consist of mostly empty space (about 99.9% of volume), which is not filled by the atomic volumes of the atoms in the gas. This results in a factor of about 1000 loss in volumetric heat capacity. Monatomic gas heat capacities per atom are also additionally decreased by a factor of two with regard to solids, due to loss of half of the potential degrees of freedom per atom for storing energy in a monatomic gas, as compared with regard to an ideal solid. There is some difference in the heat capacity of monatomic vs. polyatomic gasses, and also gas heat capacity is temperature-dependent in many ranges for polyatomic gases; these factors act to modestly (up to the discussed factor of two) increase heat capacity per atom in polyatomic gases.

The volumetric heat capacity is defined as having SI units of J/(m³·K). It can also be described in Imperial units of BTU/(ft³·F°).

Contents

Thermal inertia

Thermal inertia is a term commonly used by scientists and engineers modelling heat transfers and is a bulk material property related to thermal conductivity and volumetric heat capacity. For example, this material has a high thermal inertia, or thermal inertia plays an important role in this system, which means that dynamic effects are prevalent in a model, so that a steady-state calculation will yield inaccurate results.

The term is a scientific analogy, and is not directly related to the mass-and-velocity term used in mechanics, where inertia is that which limits the acceleration of an object. In a similar way, thermal inertia is a measure of the thermal mass and the velocity of the thermal wave which controls the surface temperature of a material. In heat transfer, a higher value of the volumetric heat capacity means a longer time for the system to reach equilibrium.

The thermal inertia of a material is defined as the square root of the product of the material's bulk thermal conductivity and volumetric heat capacity, where the latter is the product of density and specific heat capacity:

I=\sqrt{k \rho c}

See also Thermal effusivity

SI units of thermal inertia are J·m−2·K−1·s−1/2, also occasionally referred to as Kieffers,[2] or more rarely, tiu.[3]

For planetary surface materials, thermal inertia is the key property controlling the diurnal and seasonal surface temperature variations and is typically dependent on the physical properties of near-surface geologic materials. In remote sensing applications, thermal inertia represents a complex combination of particle size, rock abundance, bedrock outcropping and the degree of induration. A rough approximation to thermal inertia is sometimes obtained from the amplitude of the diurnal temperature curve (i.e., maximum minus minimum surface temperature). The temperature of a material with low thermal inertia changes significantly during the day, while the temperature of a material with high thermal inertia does not change as drastically. Deriving and understanding the thermal inertia of the surface can help to recognize small-scale features of that surface. In conjunction with other data, thermal inertia can help to characterize surface materials and the geologic processes responsible for forming these materials.

Thermal inertia of the oceans is a major factor influencing climate commitment, the degree of global warming predicted to eventually result from a step change in climate forcing such as a fixed increase in the atmospheric concentration of a greenhouse gas.

Constant volume and constant pressure

For gases it is useful to distinguish between volumetric heat capacity at constant volume and at constant pressure. This distinction has the same meaning as for specific heat capacity.

References

  1. ^ U.S. Army Corps of Engineers Technical Manual: Arctic and Subarctic Construction: Calculation Methods for Determination of Depths of Freeze and Thaw in Soils, TM 5-852-6/AFR 88-19, Volume 6, 1988, Equation 2-1
  2. ^ http://scienceworld.wolfram.com/physics/ThermalInertia.html Eric Weisstein's World of Science - Thermal Inertia
  3. ^ Thermal inertia and surface heterogeneity on Mars, N. E. Putzig, University of Colorado Ph. D. dissertation, 2006, 195 pp.

See also